Una percentuale è una frazione di una certa quantità e rappresenta quindi una grandezza adimensionale in quanto espressa come rapporto tra due grandezze omologhe. Per esprimere una quantità come percentuale di una seconda scelta come riferimento occorre dividere la prima per la seconda e poi moltiplicare per 100. Se si vuole determinare una certa percentuale di una quantità nota occorre moltiplicare il numero percentuale per la quantità e poi dividere per 100. Spesso è molto utile semplificare prima della moltiplicazione, ad esempio elidendo uno O al numeratore e uno al denominatore. Nel seguito illustreremo alcuni esempi per calcolare sconti e interessi; ricorrere a una percentuale o usare una proporzione sono spesso procedure analoghe, ognuno può decidere di usare quella che risulta più congeniale.
Se si vuole sapere il numero 40 che percentuale è di 80 si calcola: (40/80)·100 = 0,5·100 = 50%.
Se si vuole calcolare il 20% di 96 si calcola (20 · 96)/100 = (2 · 96)/10 = 2 · 9, 6 = 19,2.
- Sconti Se un collo del costo iniziale di 840 € è venduta al 15% di sconto qual è il prezzo di vendita? Ci sono due modi di procedere: o calcolare lo sconto e poi sottrarre la quantità dal prezzo iniziale per determinare il prezzo di vendita o calcolare la percentuale del prezzo iniziale come 100- percentuale di sconto e poi calcolare la percentuale ottenuta del prezzo iniziale. Mostriamo la seconda procedura: in questo caso la percentuale del prezzo iniziale è 100% -15% = 85%. Il prezzo di vendita si calcola quindi come (85 · 840)/100 = (85 · 84)/10 = 714 €.
- Capitali e interessi Se su un capitale di 2500 € si ha un interesse semplice del 4% su base semestrale, quale somma si ritira dopo 3 anni di giacenza? Innanzitutto occorre determinare quante unità temporali utilizzate per stabilire l’interesse sono contenute nell’intervallo di tempo considerato. Come prima cosa, quindi, bisogna convertire gli anni in semestri. Poiché in un anno ci sono 2 semestri si ha che 3 anni sono pari a 6 semestri.
Dopo un semestre la somma ritirata, chiamata montante M, è composta dal capitale iniziale C più gli interessi I: M = C + I. In regime di interesse semplice dopo n periodi il montante si calcola con la formula M(n) = C · (1 + i)n , dove i è il tasso di interesse. Nell’esempio i= 4% = 0,04, quindi M(6) = 2500 · (1 + 0,04)6 ≈ 3163 €. Gli interessi I sono dati da M – C = 3163 -2500 = 663 €.
La percentuale di una percentuale è pari al prodotto delle percentuali. Ad esempio il 20% del 20% di una quantità X è pari a (20/100) · (20/100) · X, cioè è il 4% di X. Restando in tema di interessi, un errore tipico che si commette è quello di non considerare adeguatamente le percentuali successive, ossia il corretto ammontare di una grandezza che varia due volte di una certa percentuale.
- Variazioni percentuali successive Se un investitore possiede 200 azioni di una compagnia che dopo una settimana hanno incrementato il loro valore del 5%, quanto guadagna alla fine sella seconda settimana se durante gli ulteriori 7 giorni le azioni subiscono un decremento di valore pari al 5%? Qualcuno potrebbe affermare che non conoscendo il valore iniziale non si può determinare quello finale, ma la considerazione è errata perché se il quesito chiede un guadagno o una perdita percentuale si hanno tutte le informazioni per individuare la risposta corretta. Tipicamente verrebbe da rispondere che se l’aumento e la diminuzione di valore sono avvenute con la stessa percentuale al termine del periodo il valore finale deve coincidere con quello iniziale. Questa conclusione, però, è errata. Per verificarlo calcoliamo separatamente le due variazioni e indichiamo con X il valore iniziale del pacchetto azionario, X1 il valore dopo una settimana e X2 quello dopo due settimane.
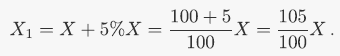
La quantità che varia durante la seconda settimana non è più X ma X1 . Quindi
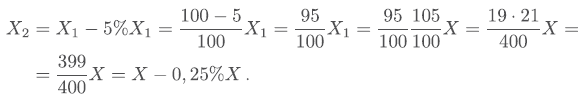
Sapendo che la frazione finale è 399 / 400 si capisce che si è persa una parte su 400, cioè un quarto di percentuale. Si noti che il numero di azioni possedute non è stato rilevante ai fini del calcolo. Si noti inoltre che se si inverte l’ordine delle variazioni, cioè se si ha prima un aumento percentuale e poi un decremento della stessa percentuale, il risultato coincide con quello trovato. Se una stessa quantità aumenta e successivamente diminuisce della stessa percentuale, il valore finale è sempre minore di quello iniziale. Lo stesso accade anche se prima diminuisce e poi aumenta della stessa percentuale. Mostriamo la seconda evenienza:
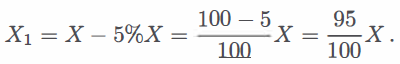
La quantità che varia durante la seconda settimana non è più X ma X1 . Quindi
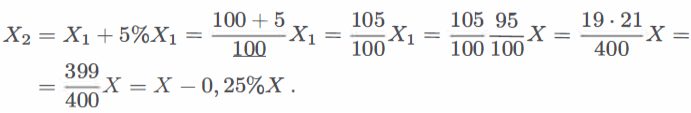
La proprietà dimostrata deriva dalla proprietà commutativa della moltiplicazione: calcolare una percentuale corrisponde a moltiplicare per una frazione e cambiando l’ordine dei fattori non si modifica il risultato finale. Concludiamo la sezione con l’utile (Tab. 05.07.02.01) che illustra alcune uguaglianze tra frazioni, percentuali e decimali. Le ultime quattro entrate sono ottenute semplicemente come multipli di relazioni precedenti, ad esempio 2/5 è il doppio di 1/5 e così via.