Molto spesso si incontrano quesiti le cui proposizioni legano queste tre grandezze cinematiche. Indicando lo spazio percorso con d dall’iniziale della parola distanza, il tempo trascorso con la t e la velocità mantenuta costante con la v si hanno le seguenti relazioni:
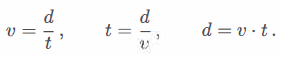
I quesiti si risolvono utilizzando una di queste relazioni, le tecniche delle equazioni di primo grado e un po’ di ragionamento. Conviene tradurre il testo in equazione e risolverla con le formule date piuttosto che guardare subito le alternative.
Se un atleta percorre 100 m in 10 s, mentre un altro ha una velocità massima di 8m/s, quale vantaggio deve avere il secondo atleta per essere sicuro di vincere?
Troviamo il vantaggio minimo, ossia quello per il quale i due atleti arrivano nello stesso momento al traguardo. Come si arguisce dalla frase, la condizione si basa sulla grandezza tempo, quindi sulla formula t = d/v. Dobbiamo uguagliare il tempo del primo atleta, cioè 10 s, con la formula del tempo per il secondo atleta ottenendo un’equazione. La nostra incognita x è il vantaggio, legato alla distanza massima, cioè 100 m, dal fatto che la distanza che percorre il secondo atleta nei 10 s è d = 100 – x:
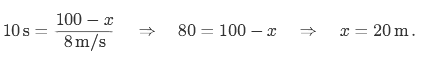
Altre volte il testo del quesito sfrutta soltanto le grandezze indicate, ma per la risoluzione occorre applicare le frazioni. Analogamente possono essere richieste l’applicazione di una percentuale o di una proporzione.
Lo stesso quesito precedente poteva essere risolto molto più semplicemente realizzando che la velocità del secondo atleta è i 4/5 di quella del primo. Se quindi devono giungere al traguardo nello stesso tempo il secondo deve percorrere una distanza pari a 4/5 di quella percorsa dal primo. Ne consegue che il vantaggio deve essere 1/5 della distanza totale, cioè 1/5 di 100 m, ovvero 100 m/5=20 m.