In realtà non esiste una vera categoria dedicata alle equazioni: come si è visto ognuna delle tecniche descritte sinora viene poi utilizzata in un’equazione. Un’equazione è un’uguaglianza in cui compare almeno un elemento ignoto, chiamato incognita (x), e almeno un termine noto (un numero). Per risolvere un’equazione di primo grado si seguono le normali regole dell’algebra e le proprietà delle operazioni. Svolte le eventuali parentesi si portano tutti i membri con l’incognita a sinistra e tutti i termini noti a destra, si sommano i termini simili a destra e quelli a sinistra, si dividono ambo i membri per il coefficiente della x e si determina l’incognita. Per equazioni di grado superiore si rimanda alla sezione dedicata nella parte di matematica. Spesso con le equazioni si risolvono problemi logici di natura geometrica, in cui ad ogni grandezza geometrica si fa corrispondere un simbolo e uno di essi è di misura incognita. Vediamo un esempio:

Se un quadrato è equivalente a un rettangolo che ha la base b di 2 m e l’altezza h di 6 m, quanto misura la diagonale del quadrato?
L’incognita è qui la diagonale d. Per risolvere il quesito occorre ricordare che due figure sono equivalenti quando hanno la stessa area, che l’area del rettangolo è A_r = b · h e quella del quadrato è A_q = l² e che lato l e diagonale del quadrato sono legati dalla relazione d = l√2.

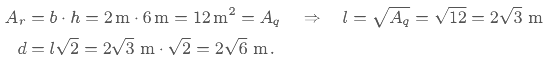
In altri casi è possibile impostare semplici equazioni per risolvere quesiti numerici. Vediamo un esempio:

Andrea, Barbara, Camilla e Dario hanno ricevuto 450000 Euro in eredità. Ad Andrea spetta il doppio di Barbara, a Camilla spetta una volta e mezza la cifra di Andrea e a Dario il triplo di Barbara. Quanto riceve Dario?

A) 100000 B) 20000 C) 50000 D) 200000 E) 150000

Leggendo la traccia notiamo che tutte le frazioni di eredità sono espresse come multipli della frazione di Barbara, che quindi poniamo uguale a x. Se la frazione di eredità di Barbara è x, allora:
frazione di Andrea = 2x;
frazione di Camilla = 2x + ½;
frazione di Dario = 3x.
Poiché l’eredità è pari a 450000 €, impostiamo la seguente equazione:
x + 2x + (2x + ½) + 3x = 450000
risolvendo per x si ottiene x = 50000, che sarà la porzione di eredità di Barbara; ma poiché il quesito chiede la porzione di Dario triplichiamo la nostra x e otteniamo 150000, ovvero la risposta E.

Il passaggio cruciale in questi quesiti è la scelta della quantità da rappresentare con l’in­cognita, perché i calcoli da svolgere per risolvere le equazioni impostate dipenderanno dai valori espressi in funzione dell’incognita scelta. Non è possibile che la risoluzione di un quesito di logica richieda di impostare un’equa­zione di secondo grado o un’altra tecnica matematica complessa; nei quesiti di logica è sempre utile puntare a soluzioni semplici. Infine, si possono anche incontrare quesiti numerici nella cui traccia compaiono delle incognite da calcolare. Possiamo indicare questi quesiti come quesiti di sostituzione, vediamo un esempio:

Un calcolatore può effettuare n calcoli in s secondi. Quanti minuti impiegherà per effettuare x calcoli?

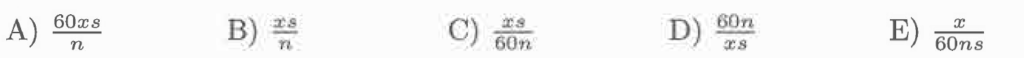
Proviamo ad interpretare le incognite nel modo seguente:

n=1 s=30 x=2

Sulla base di questa interpretazione possiamo fornire una risposta preliminare alla doman­da del quesito: se per effettuare 1 calcolo il calcolatore impiega 30 secondi, per effettuarne due impiegherà 1 minuto.
Andiamo quindi a sostituire i nostri valori all’interno delle opzioni di risposta, quella corretta sarà quella che fornisce come risultato 1, ovvero il tempo (in minuti) che secondo i nostri valori è necessario per compiere 2 calcoli:

Poiché abbiamo ottenuto un risultato ambiguo (due risposte corrette), verosimilmente la nostra interpretazione delle incognite non era la più adatta a risolvere il quesito. In questi casi è sufficiente effettuare una nuova sostituzione solo per i casi ambigui, scegliendo nuovi valori per le incognite:

n=2 s=30 x=8

In questa nuova interpretazione il calcolatore effettua due calcoli in 30 secondi e quindi per effettuare 8 calcoli impiega 2 minuti:

La risposta corretta è quindi la C.

In generale, la strategia per risolvere questo genere di quesiti è quella di sostituire dei valori ad hoc alle incognite, scelti in base ad un criterio di comodità di calcolo: sono preferibili valori che permettono di effettuare operazioni rapide, semplici e senza resto. Se la scelta è effettuata con criterio è sufficiente una sola sostituzione, altrimenti (come nell’esempio sopra) si rende necessario procedere con ulteriori tentativi.